シリンドリカルレンズを 使用する際の考察
本ページはレーザーオプティクスリソースガイドの補足セクションです
シリンダーレンズは、光を集束したり発散するのに曲面を用いているという点である種球面レンズと同じですが、一軸方向のみに光学的パワーがあり、それと直交する軸方向では光に影響を与えません。光を回転対称に一様に集束か発散させる球面レンズを用いてこれを行うことはできません。シリンダーレンズは、レーザー光のマニピュレーションや整形において重要な役割があり、レーザーのシート光形成や楕円ビームの真円化に用いられます。シリンダーレンズの非対称性の形状と特殊な製造工程の要求により、偏芯やウェッジ、および軸ツイストの規定や適切な制御が重要となります。
このため、シリンダーレンズを製造するには特殊な装置とスキル、またレンズの特徴を効果的に表す独自の基準座標系が必要になります。2つの直交方向、つまりパワー (屈折力) を持つ方向と持たない方向で基準システムを定義します。1番目の方向は「パワー方向 (Power Direction)」と呼ばれ、レンズの曲がった方向に沿ってこの軸にのみ光学的パワーが存在します (Figure 1)。2番目の方向は、光学的パワーを持たない方向に沿った「ノーパワー方向 (Non-Power Direction)」です。ノーパワー方向に沿ってシリンダーレンズの全長を延ばしても、レンズの光学的パワーに影響を与えません。シリンダーレンズは、矩形、正方形、円形、楕円形を始め、様々な形状を持たせることができます。
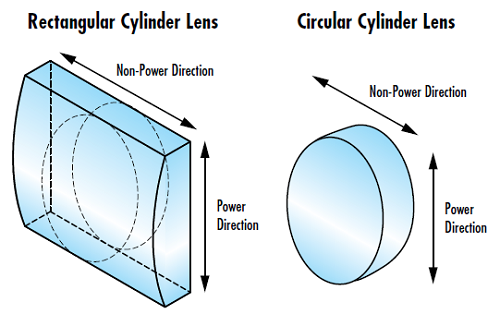
Figure 1: 矩形シリンダーレンズと円形シリンダーレンズのパワー方向とノーパワー方向
誤差や収差および仕様
完全無欠の製造工程というものは存在せず、これはシリンダーレンズの製造に関しても例外ではありません。よって、わずかな幾何学的誤差を避けることはできません。研磨工程中のミスアライメントが、シリンダーレンズに特有の機械的誤差の多くを引き起こすことがあり、この誤差によって光学的収差や性能に悪影響を及ぼします。そのため、こうした誤差を厳格に制御し、レンズの性能を保証していかなければなりません。こうした誤差は、レンズの平面側とエッジ側を含む幾何学的基準をもとに定義されます。
平面軸ウェッジ (面傾き)
理想的なシリンダーレンズでは、レンズの平面側はシリンダーの軸に平行です。レンズの平面側とシリンダーの軸間の角度的なずれは、ウェッジとして知られており、一般的には弧度法の分を単位に測定されます(Figure 2)。この角度は、レンズの両端の厚さを測定し、そこから角度を計算することで定量化されます。ウェッジは、ウインドウ (平行平面板) のウェッジ (平行度) と同様、ノーパワー方向でのイメージシフトにつながります。
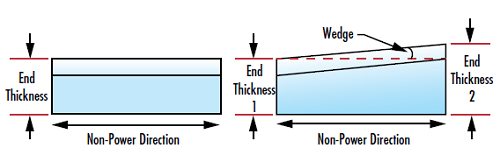
Figure 2: シリンダーレンズのノーパワー方向におけるレンズ端の厚さの違いから生じるウェッジの極端な例
パワー軸ウェッジ (偏芯)
曲面側の光軸は、理想的なシリンダーレンズではレンズのエッジに平行です (Figure 3)。球面オプティクスでの光学的パワーを持つ面の偏芯と同様に、シリンダーレンズの偏芯は、レンズのコバ面を基準にした光軸の角度的ずれになります。この角度ずれ (α) は、レンズの光軸と機械軸を不一致にさせ、ビームの偏角がつながります。レンズのコバ面が取り付け基準に用いられると、このエラーは光学的アライメントを極めて困難にさせます。しかしながら、レンズのコバ面が取り付け基準として信頼できなければ、レンズを正確な方向に傾けることによりこのエラーを取り除くことはできます。シリンダーレンズの直径が大きくなるほど、所定の偏芯角におけるレンズコバ面の厚さの違いはより大きくなります。

Figure 3: シリンダーレンズのパワー方向におけるレンズ端の厚さの違いから生じる偏芯誤差の例
軸ツイスト (ねじれ)
軸ツイストは、シリンダー軸とレンズ端面間の角度的ずれを表します。軸ツイストは、シリンダーレンズの外寸に対するパワー面の回転を意味し、これがあると、光学面に対する像の回転につながります。これは、矩形状のレンズ素子をその形状に合わせて設置する際のアプリケーションでとりわけ有害になります (Figure 4)。シリンダーレンズを回転してシリンダー軸の向きを再調整すれば、軸ツイストは補正することができます。
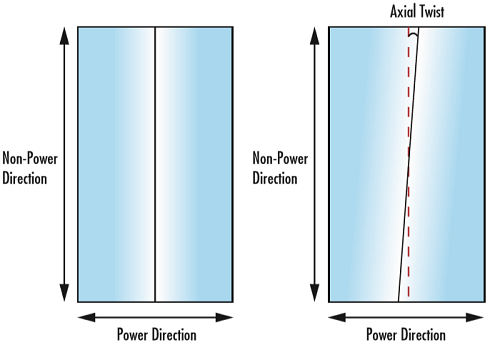
Figure 4: シリンダーレンズの軸ツイスト
アプリケーション
シリンダーレンズは、非対称なビーム形状の補正やライン光の形成、またシート光の生成など、レーザービーム整形に主として用いられます。粒子画像速度測定法 (PIV) やレーザー誘起蛍光法 (LIF) といった最新の科学手法では、細いレーザーラインや均一なレーザーシート光が要求されます。構造化照明用 (光切断用) のレーザー光も、スキャンニングや計測、アライメントのアプリケーションにとって重要なツールです。低価格なレーザーダイオードが入手可能な今、別の共通するアプリケーションにダイオードから出射された楕円状ビームからコリメートされた対称ビームを作り出すビームの真円化があります。
シート光の形成
シート光 (ライトシート) は、X軸とY軸の両方向に発散するビームです。シート光は、光軸に直交する矩形状のフィールドで、伝搬距離が長くなるにつれてこのフィールドは拡がっていきます。シリンダーレンズを用いて生成されるレーザーラインもシート光と見なすことができますが、そのシートは三角形状に拡がります。
2つの発散軸を持つ真のレーザーシート光を形成するには、凸か凹の一組のシリンダーレンズをシリンダー軸が互いに直交するように配置します (Figure 5)。各レンズが各々の軸に対して機能し、両方のレンズが組み合わさることで発散するシート光が作り出されます。
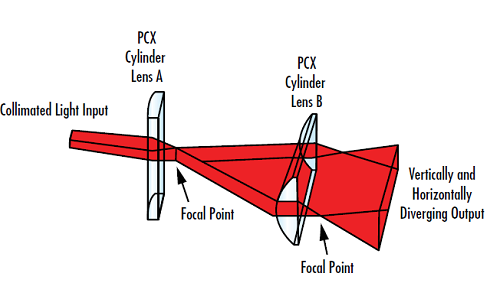
Figure 5: 矩形のシート光を生成するのに用いられる直交配置した一組のシリンダーレンズ
ビームの真円化
コリメートするオプティクスを搭載しないレーザーダイオードは、非対称なビームパターンで発散します。球面光学素子ではこれを真円コリメートビームに変えることはできません。同素子の場合、両方の軸に対して光学的パワーが同時に働き、元々の非対称性を維持してしまうからです。一組のシリンダーレンズを互いのシリンダー軸が直交するようにして用いると、各軸を独立して処理できるようになります。
対称な出射ビームを得るには、2枚のシリンダーレンズの焦点距離の比をX軸とY軸方向のビーム拡散の比に合わせる必要があります。標準的なコリメーションと同様に、ダイオードを両方のレンズの焦点上に配置し、2枚のレンズを焦点距離の差分だけ離して配置します (Figure 6)。
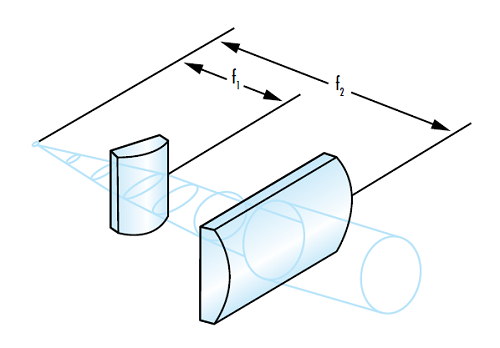
Figure 6: シリンダーレンズを用いた楕円ビームの真円化
レーザーダイオードは非常に大きな発散を持つものがあり、コリメートするのが難しくなる場合があります。なぜなら、発散の大きさがシステムの許容長さとレンズに求めるサイズに直接的な影響を与えるからです。各素子の相対位置は、その焦点距離により概ね決まるため、レンズの焦点距離 (f) とコリメートする軸側のビーム拡がり角 (θ) を用いて各レンズでの最大ビーム幅 (d) を計算することが可能になります。各レンズの有効径は、この最大ビーム幅よりも大きくしなければなりません。













 前のセクション
前のセクション 














もしくは 現地オフィス一覧をご覧ください
クイック見積りツール
商品コードを入力して開始しましょう
Copyright 2023, エドモンド・オプティクス・ジャパン株式会社
[東京オフィス] 〒113-0021 東京都文京区本駒込2-29-24 パシフィックスクエア千石 4F
[秋田工場] 〒012-0801 秋田県湯沢市岩崎字壇ノ上3番地