ガラス内のバルクレーザー損傷
本ページはレーザーオプティクスリソースガイドのセクション14.2です
Most of the literature on laser-induced damage threshold (LIDT), including that previously published by Edmund Optics®, has focused exclusively on issues related to surface damage (Figure 1). This focus was justified because, historically, the LIDT of optical components was limited by dielectric coatings and surface quality, rather than bulk damage.1 However, with the recent development of nano-structured anti-reflective surfaces, dielectric coatings are not always necessary. For these new optical elements, the LIDT now approaches the bulk damage threshold of the glass. Because of the absence of surface coatings, contamination, and defects, the surface breaks down by the same mechanism as in the bulk of the glass.2 Therefore, it is important to explore the underlying causes of bulk damage in optical glass to better understand why the LIDT is so much higher for optics with nano-structured anti-reflective.
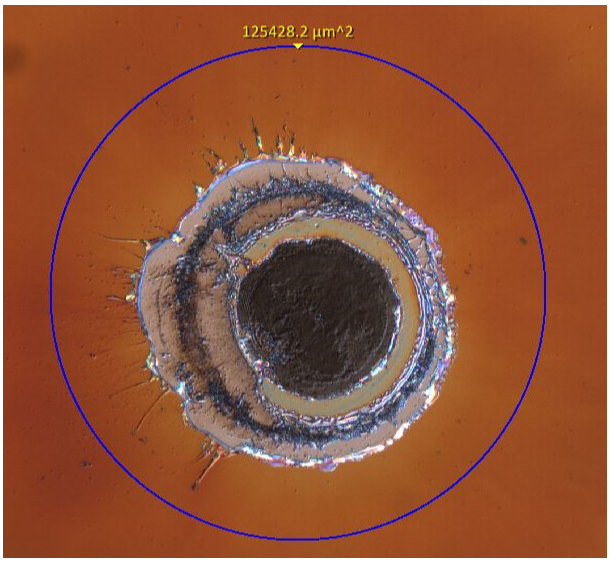
Figure 1: Surface laser-induced damage of a laser optic with a traditional thin-film anti-reflective coating. Uncoated optics, such as those with nano-structured anti-reflective surfaces, have a higher LIDT that approaches that of the bulk material.
Causes of Bulk Damage
Bulk LIDT is not only proportional to the peak power of the laser, but also scales with wavelength, beam diameter, and, most importantly, the pulse duration.1 To gain an intuitive understanding of how and why these parameters are so important, one needs to look no further than the absorption probability density function:3
In this equation, Wi represents the probability of a photon being absorbed and generating an electron in the condition band, $ \small{\phi} $ is the mean photon flux density, and $ \small{\sigma} $ is the transition cross-section, which itself is a function of the laser frequency, $ \small{\nu} $. It is important to note that while the transition cross-section, which is directly proportional to the absorption coefficient, is extremely small throughout the optical spectrum for most glasses, it is still non-zero. Therefore, when the intensity of the laser is large enough, significant absorption can take place, resulting in localized heating. This is particularly true for optical glasses that contain inclusions such as platinum, which can be deposited during the production process.4
Optical breakdown (bulk damage) occurs when a sufficiently large number of electrons are excited from the valance band to the conduction band that the free electron density in the material is large enough that it triggers nonlinear absorption inducing electron avalanche ionization.2 The combination of multiphoton absorption and impact ionization during avalanche ionization deepen the wavelength dependence of LIDT since the critical free electron density is proportional to the square of the laser frequency according to the following relationship:5
In this relationship, $ \small{n} $ is the critical free electron density, $ \small{\varepsilon} $ is the material permittivity, $ \small{m_c} $ is the reduced mass of an electron in the conduction band, and $ \small{e} $ is the charge of an electron.
While thermal breakdown due to avalanche ionization is the primary cause of optical breakdown with q-switched lasers, that is not the case with all pulsed lasers. For mode-locked lasers, with pulse durations less than approximately 20ps, a different physical phenomenon dominates. Ultrafast laser pulses are so short that the material does not have enough time to heat through localized absorption. Instead, bulk optical damage results from a process known as a Coulomb explosion. A Coulomb explosion occurs from a buildup of an electrostatic force strong enough to break the molecular bonds and cause lattice fracturing from the extremely high electric field within the ultrafast laser pulses.6
LIDT Scaling
Pulse Duration
As a general rule of thumb, LIDT due to avalanche ionization is roughly proportional to $\tau ^{\small{1/2}}_p $, where $\tau ^{\small{1/2}}_p $ is the pulse duration. This is because the multiphoton absorption process is proportional to the intensity squared and, therefore, the square root of the pulse duration.1 Once Coulomb explosions become the dominant failure mechanism, the LIDT is no longer proportional to $\tau ^{\small{1/2}}_p $. In cases such as these, the LIDT continues to decrease with pulse duration, but at a reduced rate.
Wavelength
LIDT also decreases as a function of wavelength, but not according to direct proportionality. Instead, the LIDT results from a convolution of the mean photon flux density, transition cross-section, and critical free electron density, all of which are wavelength dependent. For example, the bulk LIDT for potassium dihydrogen phosphate (KDP) is 24 $ \small{\tfrac{\text{J}}{\text{cm}^2}} $ at 1064nm and a 3ns pulse duration; at the first harmonic (532nm) the LIDT drops to 20 $ \small{\tfrac{\text{J}}{\text{cm}^2}} $ , and at the third harmonic (355nm) the LIDT is 11 $ \small{\tfrac{\text{J}}{\text{cm}^2}} $, and at the fourth harmonic (266nm) the LIDT is 3 $ \small{\tfrac{\text{J}}{\text{cm}^2}} $.7 This results in scaling factors of 0.83 from 1064nm to 532nm, 0.46 from 1064nm to 355nm, and 0.13 from 1064nm to 266nm, which highlights the difficulty in determining a single scaling factor for wavelength dependence. The wavelength scaling of the LIDT of KDP is comparable to other optical materials, like bulk and AR-coated fused silica, which has been shown to exhibit a scaling factor between 0.42 and 0.56 between 1064nm and 355nm.1
Beam Diameter
The scaling relationship between beam diameter and LIDT is even more challenging to predict. This is because, contrary to intuition, a smaller beam diameter will not result in a lower LIDT. There are two primary reasons for this. First, LIDT is specified by fluence, which is in units of $ \small{\tfrac{\text{J}}{\text{cm}^2}} $; therefore, beam diameter is already built into the value. In fact, in most cases, a smaller beam diameter ends up resulting in a larger LIDT because the beam will interact with a lower number of inclusions in the optical path. While we will not discuss either of these effects in detail here, it is essential to note that determining the actual spot size in the material can be rather challenging because Gaussian beam properties need to be taken into account along with nonlinear effects such as self-focusing.5 More information can be found in our Importance of Beam Diameter on Laser Damage Threshold application note.
Number of Shots
Bulk LIDT may be dependent on the number of shots incident on the glass. This is because some glasses, such as BK7, have a decay lifetime from the conduction band to the valance band sufficiently long enough for a pulse-to-pulse build-up of electrons. This can be experimentally observed by looking at the bulk damage point that occurs during the laser pulse.5 However, not all materials exhibit this property. For example, fused silica does not seem to demonstrate any correlation between the number of shots and bulk damage threshold.8 It is useful to note that experiments at Sandia National Labs have shown the single-shot bulk LIDT for BK7 is 4,125 $ \small{\tfrac{\text{J}}{\text{cm}^2}} $, but after only 31 pulses BK7 drops to 3,289 $ \small{\tfrac{\text{J}}{\text{cm}^2}} $. In comparison, fused silica remains constant at 3,800 $ \small{\tfrac{\text{J}}{\text{cm}^2}} $ regardless of the number of shots.5, 8 Both tests were performed using an 8ns pulse duration, 1064nm laser, and focused spot diameters between 8-16μm at the focus, facilitating a reasonably good comparison between the two materials.
Our Laser Induced Damage Threshold Scaling Calculator approximately scales an LIDT value from one wavelength, pulse duration, and beam diameter to a new set of use parameters.
Bulk LIDT of Common Glasses
In a 2013 press release, SCHOTT released a rather comprehensive analysis of the bulk damage threshold of common optical glasses.9 This experiment utilized two different 1064nm lasers, one with a pulse duration of 12ns and the other with a pulse duration of 74ps. In each case they reported the LIDT for both the fundamental and second harmonics, providing four different bulk LIDT values for each glass. This experiment was conducted with a much larger spot size at the focus, 33-41μm, than the data presented in the previous section, resulting in a slightly lower LIDT. Additionally, the data from SCHOTT was measured using Suprasil CG fused silica, whereas the earlier data was collected from Corning 7940 fused silica. The table below shows the final results for the multi-shot (>1,800 pulses) bulk LIDT of each glass, as reported by SCHOTT.9, 10 The bulk damage thresholds shown in Table 1 may vary in practice due to a variety of factors including variance in glass chemistry, finite thickness of optical components, etc. Optics may also appear damaged due to surface-level effects even if no bulk laser-induced damage occurred. Please contact us if you are uncertain about the LIDT of a particular optic.
| LIDT $ \left( \small{\tfrac{\text{J}}{\text{cm}^2}} \right) $ |
||||
| 硝種 | 1064nm @ 12ns | 532nm @ 10ns | 1064nm @ 74ps | 532nm @ 74ps |
| N-BK7 | 2017 | 74.4 | 31.8 | 8.2 |
| N-FK5 | 1574 | 226 | 35.2 | 9.7 |
| F2 | 690 | 7.7 | 16.7 | 3.5 |
| N-LASF44 | 720 | 18.5 | 13.8 | 3.7 |
| N-LAF21 | 933 | 15.0 | 12.6 | 4.7 |
| SF6 | 185 | Surface Damage | 6.4 | Surface Damage |
| Fused Silica | 1866 | 280 | 39.2 | 11 |
Table 1: Comparison of LIDT for common optical glasses used in high power laser applications.9
Understanding Bulk Laser-Induced Damage
Now that we have established a firm understanding of both the underlying physical phenomena that lead to bulk damage in optical materials, the vast number of variables involved, and the scaling relationships, we can start to better understand the results shown in Table 1. The data clearly shows that, as expected, the LIDT decreases dramatically as wavelength and pulse duration decrease. Furthermore, in most cases (except for SF6 at 532nm) the bulk LIDT threshold is far higher than the surface LIDT. It also shows that in general, crown glasses are preferable to flint glasses for high-power laser applications. Generally, fused silica outperforms either category across a wide range of laser parameters.
The difference between bulk and surface LIDT becomes even starker when compared to a typical V-coated fused silica laser window, which is generally on the order of tens of $ \tfrac{\text{J}}{\text{cm}^2} $. Also, it has been shown that for fused silica, with a well-polished and uncoated surface, the surface LIDT is approximately equal to the bulk LIDT.8 As a result, the LIDT of fused silica laser optics with nano-structured anti-reflective surfaces is significantly higher than that of traditional V-coated optics.
Learn More About Laser-Induced Damage
- レーザーコンポーネントにおけるレーザー誘起損傷閾値 (LIDT) の理解と規定
- レーザー損傷閾値試験
- 超短パルスレーザーのLDT
- Laser Damage Threshold Calculator
- LDTにおけるビーム径の重要性
参考文献
[1] Koechner, W., 1999. Solid-state laser engineering (Vol. 1). Springer.
[2] Bloembergen, N., 1974. Laser-induced electric breakdown in solids. IEEE Journal of Quantum Electronics, 10(3), pp.375-386.
[3] Saleh, B.E. and Teich, M.C., 2019. Fundamentals of photonics. John Wiley & Sons.
[4] Bloembergen, N., 1970. Fundamentals of Damage in Laser Glass. National Materials Advisory Board Publication NMAB, 271.
[5] Kimmel, M., Do, B.T. and Smith, A.V., 2011, November. Deterministic single shot and multiple shot bulk laser damage thresholds of borosilicate glass at 1.064 micron. In Laser-Induced Damage in Optical Materials: 2011 (Vol. 8190, p. 81900Z). International Society for Optics and Photonics.
[6] Wang, D.N., Wang, Y. and Liao, C.R., 2015. Femtosecond laser micromachining on optical fiber. In Laser Surface Engineering (pp. 359-381). Woodhead Publishing.
[7] Rainer, F., Atherton, L.J. and De Yoreo, J.J., 1993, June. Laser damage to production-and research-grade KDP crystals. In 24th Annual Boulder Damage Symposium Proceedings--Laser-Induced Damage in Optical Materials: 1992 (Vol. 1848, pp. 46-58). International Society for Optics and Photonics.
[8] Smith, A.V. and Do, B.T., 2008. Bulk and surface laser damage of silica by picosecond and nanosecond pulses at 1064 nm. Applied optics, 47(26), pp.4812-4832.
[9] Schott AG. (2013) SCHOTT Identifies Alternative Glass Materials for High-Power Laser Applications [Press release]. 5 February. Available at: <https://www.us.schott.com/newsfiles/us/20130204193642_schott_laser-resistant_optics_final.pdf>.
[10] Jedamzik, R., Dietrich, V. and Rossmeier, T., 2012. Bulk Laser Damage Threshold of Optical Glasses. In Proceedings of DGaO (Vol. 113, p. B9).













 前のセクション
前のセクション 

もしくは 現地オフィス一覧をご覧ください
クイック見積りツール
商品コードを入力して開始しましょう
Copyright 2023, エドモンド・オプティクス・ジャパン株式会社
[東京オフィス] 〒113-0021 東京都文京区本駒込2-29-24 パシフィックスクエア千石 4F
[秋田工場] 〒012-0801 秋田県湯沢市岩崎字壇ノ上3番地