幾何光学入門: 近軸光線追跡計算

Geometrical Optics 101: Paraxial Ray Tracing Calculations

光線追跡は、光学エンジニアが光学系の性能を決定するために用いる主要な方法です。光線追跡は、各面での屈折/反射の角度を計算することで、システムを通過する光線を手作業で追跡することです。この方法は、ガウスやニュートンの結像式がその複雑度合いから適さない、多くの面を有するシステムでは非常に有益です。

今日、光学エンジニアは、ZEMAX^®やCODE V^®等の光線追跡ソフトウェアを用いることで、非常に複雑なシステムの性能を迅速にシミュレーションできるようになっています。近軸光線追跡は、小さな光線角度と高さが関係します。近軸光線追跡の基本的な原理を理解するために、システムを通過する光線を手作業で追跡する際に必要な計算と光線追跡シートの活用を検討します。これにより、現代のコンピューティングソフトウェアの有用性が強調されることになります。

近軸光線追跡の手順：平凸レンズのバックフォーカスを計算

通常、手作業による近軸光線追跡は、光線追跡シートを用いて行われます (Figure 1) 。光学レンズの面の数を水平方向に、主要なレンズパラメータを垂直方向に記載した表です。また、マージナル光線と主光線を区別するパラメータもあります。Table 1に、主要な光学レンズパラメータを解説します。

手作業による近軸光線追跡の手順を解説するため、平凸レンズで考えてみることにします。この例では、簡単にするために、#49-849 25.4mm径 x 50.8mm FL のレンズを使用します。この特定の計算は、平凸レンズのバックフォーカス $ \small{ \left( \text{BFL} \right)} $ を計算するために用いられていますが、光線追跡法は、基点から瞳のサイズやその位置まで、さまざまなシステムパラメータを計算するために用いることができる点にもご留意ください。

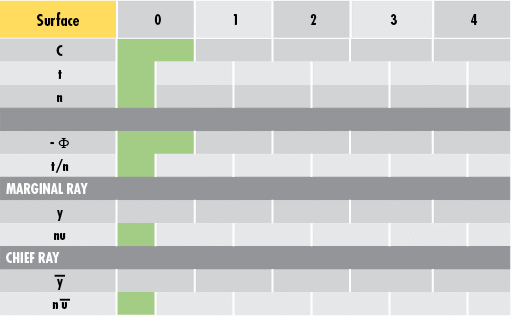
Figure 1: 光線追跡シートの例

ステップ 1: 既知の値を入力

最初に、#49-849の既知の寸法値を光線追跡シートに入力します (Figure 2)。面0は物体面、面1がレンズの凸面、面2がレンズの平面で、面3が像面になります (Figure 3)。

なお、曲率 $ \small{ \left( C \right)} $ は、1を曲率半径 $ \small{\left( R \right)} $ で割った値に等しくなります。最初の厚さの値 $ \small{ \left( t \right)} $ (この例では25mm) は、物体からレンズの第一面までの距離です。平行光 (つまり、光学レンズの光軸に対して平行な光) が入射する場合、この値は任意になります。屈折率 $ \small{ \left( n \right)} $ は、空気ではおおよそ1、レンズのN-BK7基板では1.517になります。

変数	説明
$$ C $$	曲率
$$ t $$	厚さ
$$ n $$	屈折率
$$ \Phi $$	面屈折力
$$ y $$	光線高さ
$$ u $$	光線角度

Table 1: 光線追跡での光学レンズパラメータ

Figure 2において、赤枠で示した箇所がレンズの第二面から焦点 (BFL) までの距離なので、計算される値になります。面個々の屈折力 $ \left( \Phi \right) $ が4行目で与えられ、公式 (1) を用いて計算されます。補足：計算をさらに容易にするため、この行に負の符号が加わります。本例では、面1がシステム内で唯一の曲面になるため、屈折力をもつ唯一の面となります。

(1)$$ \Phi = \left( n_2 - n_1 \right) C_1 $$

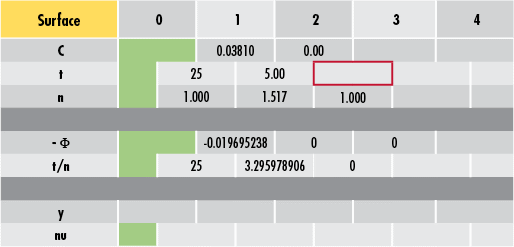
Entering Known Lens Parameter Values into Ray Tracing Sheet

Figure 2: 既知のレンズパラメータ値を光線追跡シートに入力

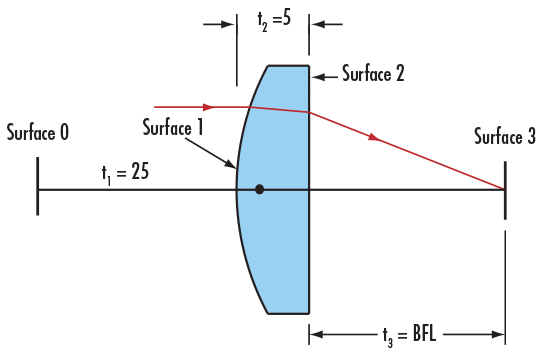
Figure 3: 平凸レンズの各面

ステップ 2: システムにマージナル光線を追加

次のステップは、システムにマージナル光線を追加することです。平凸レンズは、曲率半径が一定の球面レンズで、コリメートされた入射ビームが用いられるため、光線の高さ $ \small{\left( y \right)} $ は任意になります。計算を簡単にするため、1mmの高さを使用します。

コリメートされたビームは、光線の最初の角度 $ \small{\left( u \right)} $ が $ \small{0}° $ であることも意味します。光線追跡シートでは、$ \small{ n \, u } $ が光線の角度にその媒体の屈折率を乗算した値です。2つの変数が後続の計算を簡単にするために含まれています (Figure 4) 。

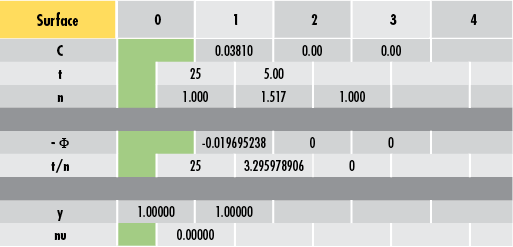
Adding a Marginal Ray to the Ray Tracing Sheet

Figure 4: 光線追跡シートにマージナル光線を追加

ステップ 3: 公式と光線追跡シートでバックフォーカスを計算

光線追跡には、屈折力を計算する方程式に加えて、2つの主要な公式が含まれます。方程式 (2) - (3) は、光線追跡計算に必要になります。

(2)$$ y' = y + u't' $$

(3)$$ n'u' = nu - y \Phi $$

ここで、アポストロフィは後続の面、角度、厚さなどを示します。この例では、面2における光線の高さ $ \small{ \left( y' \right) }$ を求めるには、面1における光線の高さ $ \small{ \left( y \right) }$ を用い、それを-0.0197 x 3.296に加算します：

(2.1)\begin{align} y' & = y + u't' \\ & = y + \left( \frac{t'}{n'} \right) n'u' \\ & = 1 + \left( 3.296 \right) \left( -0.0197 \right) = 0.93508 \end{align}

光線の角度に対してこれを実行すると、以下の値が得られます。光線追跡が完了するまで、こうしたプロセス全体が繰り返されます (Figure 5)。

(3.1)\begin{align} n'u' & = nu - y \Phi \\ & = -0.0197 + \left( 0.93508 \right) \left( -0 \right) = -0.0197 \end{align}

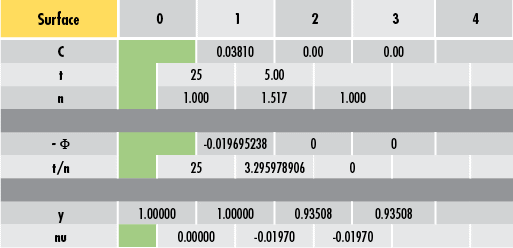
Figure 5: 光線をシステム全体にまで伝播

ここで、最終的な光線の高さが0になるまで厚さの値を調整するか (Figure 6)、あるいは光線の高さが0の場合の $ \small{\text{BFL}} $ を逆算することで、$ \small{\text{BFL}} $ を求めます。#49-849の場合、最終的な$ \small{\text{BFL}} $ の値は47.48mmになります。これは、レンズの仕様に記載されている47.50mmに非常に近い値です。この違いは、レンズが最初に設計された時に使用された値がわずかに正確な値ではなく、1.517の屈折率を用いたことによる丸め誤差に起因しています。

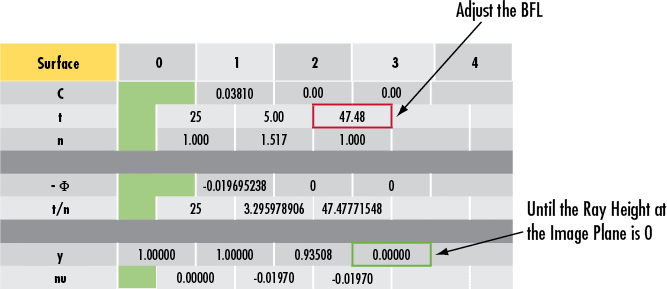
Calculating Back Focal Length of a Plano-Convex (PCX) Lens using a Ray Tracing Sheet

Figure 6: 光線追跡シートを用いて平凸レンズのバックフォーカスを計算

二枚レンズの光線追跡シートを解読

光線追跡シートを完全に理解するために、両凹レンズ、絞り、両凸レンズで構成された二枚レンズシステムを考えてみます (Figures 7-8) 。両凹レンズや両凸レンズの詳細は、光学レンズの形状を理解するをお読みください。

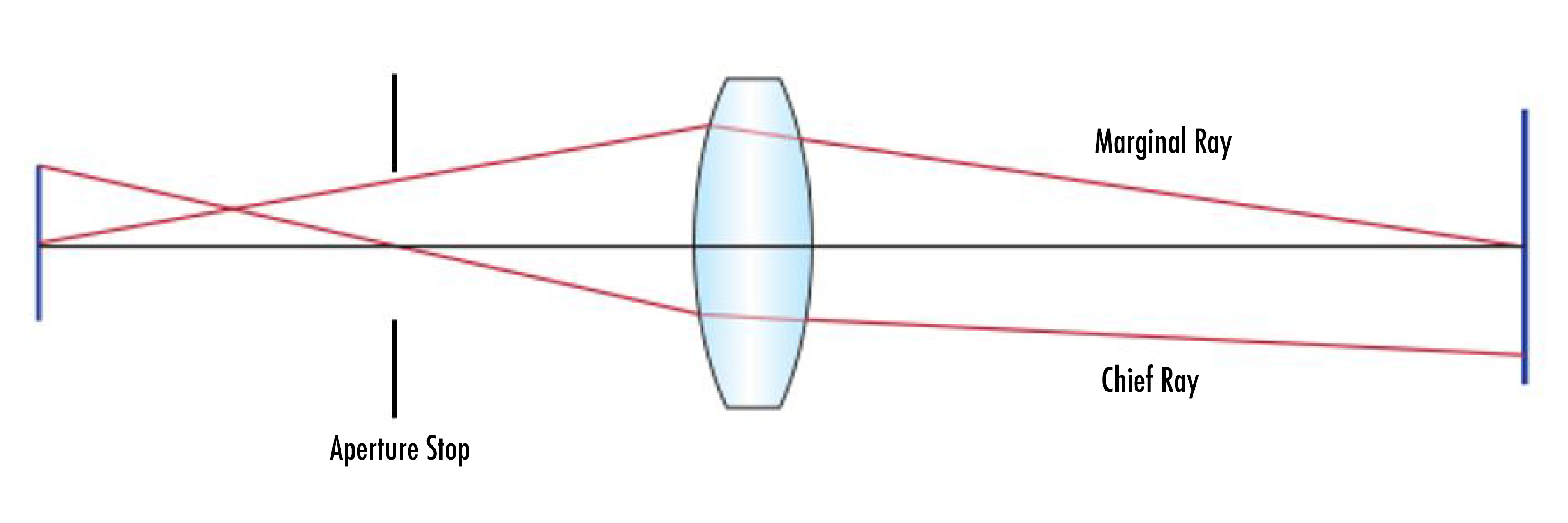
Double-Concave and Double-Convex Lens System

Figure 7: 両凹と両凸のレンズシステム

Sample Double-Concave (DCV) and Double-Convex (DCX) Ray Tracing System

Figure 8: 両凹と両凸の光線追跡システムの例

開口絞りは、制限開口を指し、システムを通過できる光の量を定義します。開口絞りは、光学レンズ面でも、また絞りでもなり得ますが、どちらにしても、常に物理的な面になります。入射瞳は、開口絞りよりも前側に配置されたレンズ素子群を通して物空間内に結像される、開口絞りの像です。射出瞳は、開口絞りよりも後側に配置されたレンズ素子群を通して像空間内に結像される、開口絞りの像です。

光学系では、開口絞りと瞳が2つの非常に重要な光線を定義するために用いられます。主光線は、物体のエッジから出発し、入射瞳、射出瞳、および絞りの中心を通過する光線です (換言して、それらの位置では高さ $ \small{\left( \bar{y} \right)} $ が0になります)。そのため、主光線は物体と像のサイズ、および瞳の位置を定義します。

光学系のマージナル光線は、物面の光軸上から出発します。この光線は、瞳のエッジに当たって停止し、物点と像点で軸を横断します。そのため、マージナル光線は物体と像の位置、および瞳のサイズを定義します。

開口絞りの位置

開口絞りの位置が不明な場合、擬似マージナル光線と呼ばれるトライアル光線をシステム内に伝播させる必要があります。物体が無限遠にない場合、この光線は物体の光軸位置から出発しなければならず、任意の入射角を持たせることができます。物体が無限遠にある場合、光線は任意の高さから出発することができ、$ \small{0} ° $ の入射角が必要になります。完了すると、開口絞りは、単純に最小の $ \tfrac{\text{CA}}{y_p} $ ($ \small{\text{CA}/y_p} $でも示され) の値を持つ面となり、ここで、$ \small{\text{CA}} $ は面の有効径で、$ \small{y_p} $ はその面における擬似マージナル光線の高さになります。

開口絞りの位置を特定した後、擬似マージナル光線を適切にスケールして実際のマージナル光線を得ることができます (繰り返しになりますが、マージナル光線は開口絞りのエッジを通る必要があります)。開口絞りのサイズと位置がわかれば、その位置では、マージナル光線の高さが絞りの半径に等しく、主光線の高さがゼロになります。次に、これらの地点から順方向と逆方向の両方に近軸光線追跡を実行することができます。逆方向に光線追跡を実行する場合、公式 (4)-(5) が有用です。公式 (2)-(3) と類似している点に留意。

(4)$$ y = y' - u't' $$

(5)$$ nu = n'u' + y \Phi $$

口径食分析

開口絞りの位置とサイズがわかった後は、口径食分析を用いてどの面に口径食が生じるか、あるいは光線が遮断されるかを確認します。口径食分析は、各面の有効径を2で割ることで行われます。次に、この値をその面における主光線とマージナル光線の高さと比較します (公式 (6))。公式 (6) は、公式 (7) に簡単に変換できます。公式 (7) が正であるなら、その面では口径食は生じません。

(6)$$ \frac{\text{CA}}{2} \geq \left| \bar{y} \right| + \left| y \right|$$

(7)$$ \frac{\text{CA}}{\left| \bar{y} \right| + \left| y \right|} \geq 2 $$

前述の両凹と両凸の例では、面3は、$ \tfrac{\text{CA}}{\left( \left| \bar{y} \right| + \left| y \right| \right)} $ の値がすべての面において最も小さくなる開口絞りとなります。また、すべての値が2以上になるため、どの面でも口径食は生じません。

物体/像のサイズと位置

物体 (面0)

サイズは直径10mm (面0における主光線高さの2倍)
位置は最初のレンズの手前5㎜の場所 (最初の厚さの値)

像 (面6)

サイズは直径18.2554mm (最終的な主光線高さの2倍)
位置は最終のレンズ面から115.4897mm後方 (最後の厚さの値)

面0の主光線高さは正で、面6の主光線高さが負になることに注意するのが重要です。これは、像が反転していることを示しています。

焦点距離

焦点距離 $ \small{ \left( \text{EFL} \right)} $ を求めるには、物体を無限遠に配置した時にシステムを通る擬似マージナル光線を追跡することがまず必要になります (即ち、最初の光線角度が0になります)。Figure 9では、計算を簡単にするため、任意の最初の高さは1が選択されています。すべて完了すると、システムの $ \small{ \text{EFL}} $ が公式 (8) で与えられます。

Figure 9: 擬似マージナル光線

(8)\begin{align} \text{EFL} & = \frac{y_1}{nu_{\text{last}}} \\ & = \frac{1}{0.02870} = 34.843 \text{mm} \end{align}

(9)\begin{align} \text{FOV} & = 2 \left( n \bar{u} \right) \\ & = 2 \left( 0.182 \right) = 0.364 \text{radians} = 20.856° \end{align}

ここで、$ \small{n \, \bar{u}} $ は最初の主光線角度です。

ラグランジュ不変量

光学不変量は、光学設計者がシステムを完全に光線追跡することなく、さまざまな値を決定できる有益なツールです。システム内の任意の軸点における2つの光線を比較することで得られます。システム内のすべての地点における任意の2つの光線に対し、光学不変量は一定です。つまり、2つの光線のセットの不変量がわかれば、一方の光線を追跡し、不変量によってそれをスケーリングすることで他方の光線を見つけます。

ラグランジュ不変量は、主光線とマージナル光線を2つの注目する光線として用いる、光学不変量のバージョンの一つです。公式 (10) を用いて求められ、Figure 10 に図解されています。

(10)$$ Ж = n \bar{u} y - n u \bar{y} $$

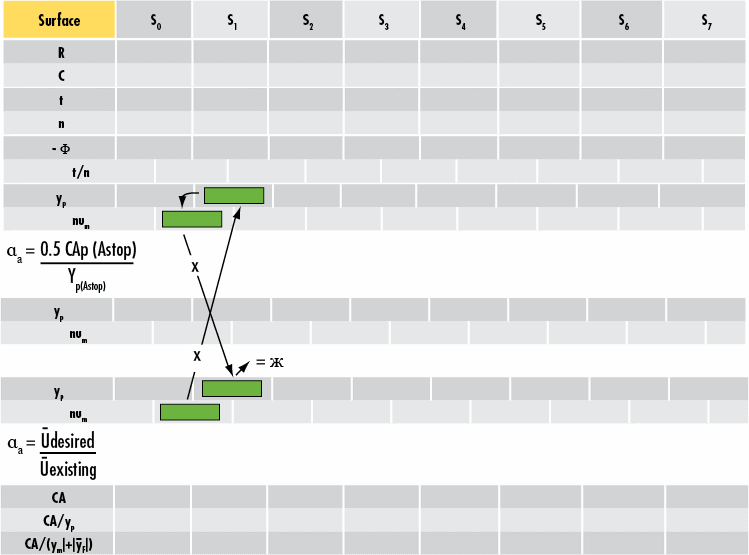
Figure 10: 光線追跡のラグランジュ不変量

実世界の光線追跡とソフトウェアのメリット

近軸光線追跡では、いくつかの仮定によって計算に誤差が生じることがあります。近軸光線追跡は、すべての角度の正接と正弦が角度自体に等しいと仮定します (換言して、$ \small{\tan{\left( u \right)} = u} $ かつ $ \small{\sin{\left( u \right)} = u} $)。角度が小さい場合にはこの近似は有効ですが、光線角度が大きくなると、誤差の伝播につながる可能性があります。

実光線追跡は、小角近似を排除し、各面のサグを考慮して軸外光線の屈折をより良くモデル化することで、近軸の誤差を低減する手法です。近軸光線追跡と同様に、光線追跡シートを使用して手作業で実光線追跡を行うことができます。簡潔にするために、近軸法のみを解説しました。CODE VやZEMAXなどの光線追跡ソフトウェアは、実光線追跡法を用いてユーザーが入力した光学系をモデル化します。

手作業による光線追跡は、面倒な作業です。そのため、光線追跡ソフトウェアが通常推奨される分析手法になります。Figure 11は、二枚レンズの光線追跡シートを解読にある両凹-両凸システムを表したものです。以下のZEMAXのスクリーンショットは、34.699mmの焦点距離値を示しており、以前に解説した近軸計算結果と同様であることが確認されます。

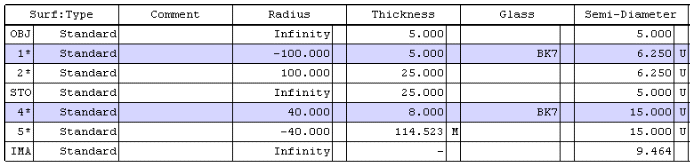
Figure 11: ZEMAXのシステムデータ例

光線追跡は、あらゆる光学設計者にとり、重要なツールです。光線追跡ソフトウェアの普及により、手作業による近軸光線追跡の必要性は最小限に抑えられますが、個別の光線がどのように光学系内を移動するかを概念的に理解するのは、依然として有用です。近軸光線追跡と実光線追跡は、設計を完成させて生産に入る前に、光学レンズの性能を概算する、素晴らしい方法です。光線追跡なしでは、システム設計が大分難しくなり、コストや時間もかかります。

参考文献

Dereniak, Eustace L., and Teresa D. Dereniak. "Chapter 10. Paraxial Ray Tracing." In Geometrical and Trigonometric Optics, 255-91. Cambridge, UK: Cambridge University Press, 2008.
Geary, Joseph M. "Chapter 4 – Paraxial World." In Introduction to Lens Design: With Practical Zemax Examples, 33-42. Richmond, VA: Willmann-Bell, 2002.
Greivenkamp, John E. "Paraxial Raytrace." In Field Guide to Geometrical Optics, 20-32. Vol. FG01. Bellingham, WA: SPIE—The International Society for Optical Engineers, 2004.
Smith, Warren J. "Chapter 3. Paraxial Optics and Calculations." In Modern Optical Engineering, 35-51. 4th ed. New York, NY: McGraw-Hill Education, 2007.