ショートパスとロングパスフィルターを用いて、「あなた仕様」のバンドパスフィルターを構築する
バンドパスフィルターは、特定の波長域もしくは波長帯を透過し、その他の波長の透過を遮断する性能を有します。多くのバンドパスフィルターが在庫販売される中、バンド幅や中心波長的に在庫販売品では対応できないアプリケーション要件では、ロングパスフィルターとショートパスフィルターを重ねて、カスタムのバンドパスフィルターを構築することができます。ロングパスフィルターは、短波長側を反射し、長波長側を透過する機能をもった光学フィルターです。これとは反対に、ショートパスフィルターは、短波長側を透過し、長波長側を反射する機能があります。両方のフィルターの分光透過曲線の一例をFigure 1に紹介します。
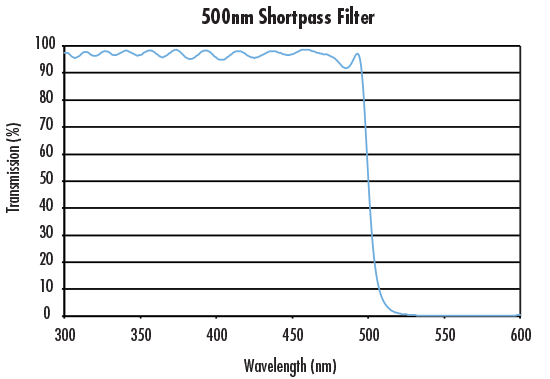
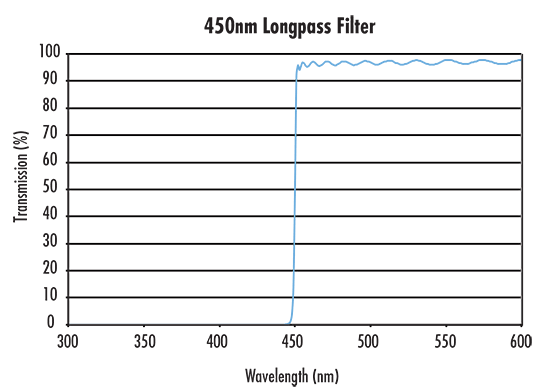
Figure 1: ショートパスとロングパスフィルターの透過曲線の比較
両者の透過曲線は、数学上のヘビサイド関数 (H(λ)) にとても類似しています。公式1に示してある通り、ヘビサイド関数は、定数 x によって決まる特定の区分線形関数です。
H(λ)はフィルターの透過率として表され、波長はλで表されます。Figure 1のロングパスフィルターの分光透過曲線のヘビサイドモデルをFigure 2に示します。
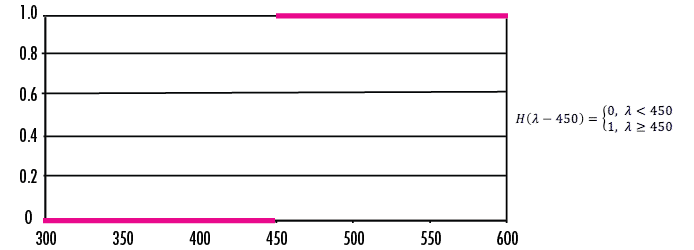
Figure 2: Figure 1のロングパスフィルターのヘビサイドモデル
1枚のカスタムバンドパスフィルターは、最低2枚のフィルターを用いることで作り出すことができます。これは、数学上のヘビサイド関数を掛け合わせるのと概念的に大変似ています。450 から 500 までに矩形関数を得たい場合、解1やFigure 3に示した通り、2つのヘビサイド関数を掛け合わせる必要があります。
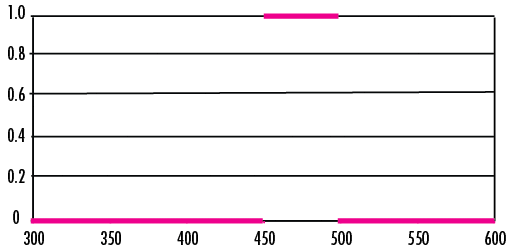
Figure 3: BP1,2の矩形関数のグラフ
数学の掛け算を用いて得られることは、2枚あるいはそれ以上の枚数の光学フィルターを物理的に重ねることで行えます。複数枚の光学フィルターを重ねると、光は最初のフィルターを通り、次のフィルターへと進みます。個々のフィルターは特定の波長しか透さないため、フィルターを重ねることで任意の波長帯だけを透過させることが可能となります。
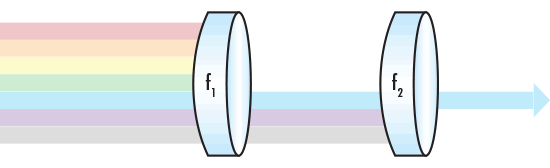
Figure 4: f1とf2 をそれぞれロングパスフィルターとショートパスフィルターにした時に構築されるカスタムバンドパスフィルター
フィルターの重ね合わせにより得られた透過曲線の結果をFigure 5 に示します。
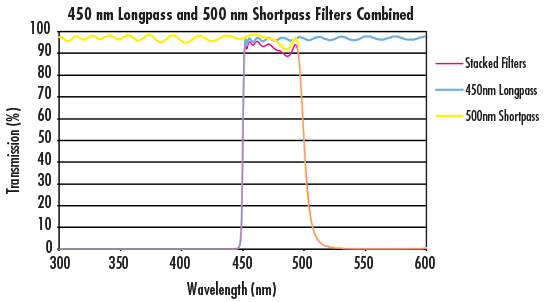
Figure 5: 450nm のロングパスと 500nm のショートパスフィルターを重ねることで作られるカスタムバンドパスフィルターの透過曲線
ロングパスとショートパスフィルターを重ねることで、特定のバンドパス特性を実現するカスタムソリューションを素早く構築することができます。このソリューションは、在庫販売品のバンドパスフィルターでは要件を満たせない場合、或いは特注でフィルターを製作すると非常に高価でリードタイム的にも長すぎる場合に、理想的と言えます。




















































































































もしくは 現地オフィス一覧をご覧ください
クイック見積りツール
商品コードを入力して開始しましょう
Copyright 2023, エドモンド・オプティクス・ジャパン株式会社
[東京オフィス] 〒113-0021 東京都文京区本駒込2-29-24 パシフィックスクエア千石 4F
[秋田工場] 〒012-0801 秋田県湯沢市岩崎字壇ノ上3番地