分散

分散は、光が光学媒質を透過する際、光学的周波数/波長といったパラメータに依存して光の位相速度もしくは位相遅延が変化する現象です。レーザーオプティクスの基板内部で生じる分散には、波長分散 (Figure 1) や多モード分散、偏波モード分散など、いくつかのタイプがあります¹。

$>Figure 1: Refractive index of UV Grade fused silica as a function of wavelength$

Figure 1: UVグレード合成石英ガラスの波長別屈折率

波長分散

屈折率は、真空中における光速と、空気やガラスなどの媒質中を通過する光波の速度比で表されます。パルスレーザーアプリケーションでは、光を波長ではなく、周波数で表すのが一般的です。なぜなら、光の波長はその大きさが通過する材料の屈折率に依存するのに対し、同アプリケーションでは時間の方が一般的により重要な概念であり、また光の周波数は固定値になるからです。波長 $ \small{\left( \lambda \right)} $ は、角振動数 $ \small{\left( \omega \right)} $、屈折率 $ \small{\left( n \right)} $、および光速 $ \small{\left( c \right)} $ と以下の関係があります：

(1)$$ \lambda = \frac{2 \pi \, c}{\omega \, n} $$

材料の屈折率は、その材料定数、$\small{B_1}$、$\small{B_2}$、$\small{B_3}$、$\small{C_1}$、$\small{C_2}$および$\small{C_3}$を係数とする次式 (セルマイヤの分散式) でよく表されます。

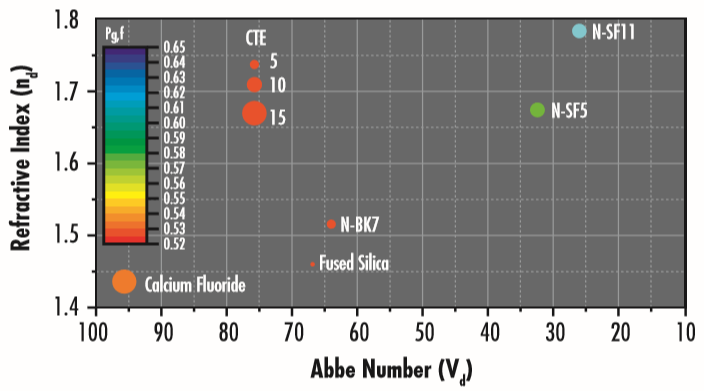
(2)$$ n^2 \! \left( \lambda \right) - 1 = \frac{B_1 \, \lambda ^2}{\lambda ^2 - C_1 } + \frac{B_2 \lambda^2}{\lambda^2 - C_2} + \frac{B_3 \lambda^2}{\lambda ^2 -C_3} $$

波長分散は、媒質内での光の速度 $\small{\nu _{p}}$の大きさが波長に依存し、大抵の場合は光と媒質内の電子間相互作用から生じます。波長分散の大きさは、アッベ数 (Figure 2) を用いて表すことができます。アッベ数は、波長 ($ \small{\lambda} $) の屈折率に対する一次偏導関数を表し、屈折率と波長間の二次偏導関数に関連した部分分散にも対応しています。

Figure 2: 主要な硝種の屈折率とアッベ数の関係を示すアッベダイアグラム図。熱膨張係数 CTE (Coefficient of Thermal Expansion) は熱膨張係数で解説される

アッベ数は次式で与えられます：

(3)$$ V_D = \frac{n_D - 1}{n_F - n_C} $$

$\small{n_D} $、$\small{n_F} $および$\small{n_C} $は、フラウンホーファースペクトルのd線 (589.3nm)、F線 (486.1nm) および C線 (656.3nm) の各波長での基板の屈折率です。材料のアッベ数は、波長の屈折率に対する導関数を用いてどの波長で表すこともできます。

(4)$$ V _{\lambda} = -\frac{1}{2} \left(n - 1 \right) \frac{\text{d} n}{\text{d} \lambda} $$

レーザーアプリケーションに対する主要な課題は、分散が媒質内を通過するレーザーパルスの特性にどのような影響を与えるかです。これは、波数に対する媒質内の光の位相速度の変動の大きさ、即ち群速度 $ \small{\nu _g} $で表されます。

(5)$$ \nu _g = \left( \frac{\partial k}{\partial \omega} \right)^{-1} = c \left[ \frac{\partial}{\partial \omega} \left( \omega n \! \left( \omega \right) \right) \right] ^{-1} = \frac{c}{n \! \left( \omega \right) + \omega \frac{\partial n}{\partial \omega}} = \frac{c}{n_g \! \left( \omega \right)} $$

ここで、波数 $ \small{ \left( k \right)} $ は$ \tfrac{2 \pi}{\lambda} $ であり、時にはスペクトル位相と呼ばれることもあります。複数の波長を含む光がある材料を通過する時、周波数 (波長) の群速度依存性から、長波長 (低周波数) の方が短波長よりもわずかながら早く通過するのが通常です² 。これにより、プリズムを通過する光が材料のスペクトル分散によって各構成色に分離されるのと同じ様に、波面の位相のスペクトル変動が生じます。群速度が周波数に対する位相速度の一次導関数として与えられるため、群速度分散 (Group Velocity Dispersion; $\small{\text{GVD}}$) は、周波数に対する逆群速度の導関数として次式のように表されます。

(6)$$ \text{GVD} = \frac{\partial}{\partial \omega} \left( \frac{1}{\nu _g} \right) = \frac{\partial}{\partial \omega} \left( \frac{\partial k}{ \partial \omega} \right) = \frac{\partial ^2 k}{\partial \omega ^2} $$

群速度は、屈折率の一次導関数が波長または周波数に対応するという点でスペクトル分散と似ており、$\small{\text{GVD}}$は、その二次導関数が波長または周波数に対応することから、部分分散と同様に用いられます。低$\small{\text{GVD}}$用のオプティクスの設計は、色補正された性能を設計するのに似ています。違う点は、アッベ数や部分分散よりもむしろ群速度や$\small{\text{GVD}}$に注目している点です。

A further discussion of $ \small{\text{GVD}} $ and its importance for ultrafast laser optics can be found in our Ultrafast Dispersion application note.

多モード分散

多モード分散は、マルチモードファイバーなどの導波路内で光の群速度や光学的周波数、また伝搬モードに依存しています²。このことは、マルチモード光ファイバー通信システムにおいては、実現可能なデータ通信速度、即ちビットレートに厳しい制限を与えることになります。多モード分散は、シングルモードファイバーか屈折率分布が放物線形状を描くGI型マルチモードファイバーを用いることで、防げる可能性があります。

偏波モード分散

偏波モード分散は、高データ通信レートのシングルモードファイバーシステムに関連するモード分散で、媒質内の光の伝搬特性が偏光状態に依存しています。こうした3種類の分散全てが、自由空間や光ファイバー内の超短パルス信号の時間的膨張や圧縮を招き、個々のパルスが混ざりあって各々が認識できなくなる可能性を引き起こします (Figure 3)。