ガウシアンビームの伝播

レーザーオプテックスアプリケーションの多くで、レーザービームは理想的ガウス分布に沿った放射強度プロファイルを持つガウシアンと想定されています。実際の全てのレーザービームは、この理想的なガウス的性質からある程度はずれています。ビーム品質係数としても知られているM²値は、現実のレーザービームの性能を回折限界のガウシアンビームのそれと比較します (ビーム品質とストレール比をご覧ください)¹。ガウシアン強度分布は、ビームの中心を軸に左右対称であり、ビームの中心から半径方向の距離が大きくなるにつれ、その強度が小さくなります (Figure 1)。この分布は、式1で表されます²。

(1)$$ I \! \left( r \right) = I_0 \exp{\left( \frac{-2 r^2}{w \left( \! z \right)^2} \right)} = \frac{2P}{\pi w \left( \! z \right)^2} \exp{\left( \frac{-2 r^2}{w \left( \! z \right)^2} \right)} $$

式1において、I₀はビーム中心でのピーク放射強度、rは軸からのラジアル方向距離、w (z)は放射強度がI₀の1/e² (13.5%) になる地点のレーザービームの半径、zは波面がフラットになる面からの伝播距離、Pはビームの全パワーになります。

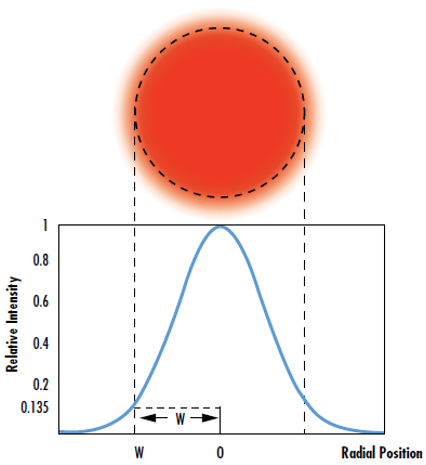
Figure 1: The waist of a Gaussian beam is defined as the location where the irradiance is 1/e<sup>2</sup> (13.5%) of its maximum value

Figure 1: ガウシアンビームのウエストは、放射強度が最大値の1/e2 (13.5%) になる地点で定義される

しかしながら、この放射強度分布は、ビームが空間を伝播する時に一定のままではなく、zの関数を含むw (z)に依存します。ガウシアンビームは、回折によってビーム直径が最小値をとるビームウエスト (w₀) と呼ばれるエリアの前後で収束し、発散します。ビームウエストの両側で発散角θの大きさで均等に収束/発散します (Figure 2)。ビームウエストと発散角の大きさはどちらも軸から測定され、その関係は式2と式3で表されます¹。

(2)$$ w_0 = \frac{\lambda}{\pi \theta} $$

(3)$$\theta = \frac{\lambda}{\pi w_0} $$

上記公式において、λはレーザーの波長、θはファーフィールド近似した発散角です。したがって、θはビームウエスト近傍でのビームの発散を正確には表しませんが、ビームウエストからの距離が増すにしたがい、より正確になります。式3から分かるように、ビームウエストが小さいと発散角は大きくなり、ビームウエストが大きいと発散角は小さく (よりコリメートビームに) なります。これは、ビームエキスパンダーをなぜ用いるかの説明にもなります。ビーム径を大きくすることでビームの発散を逆に減らすことができるからです。

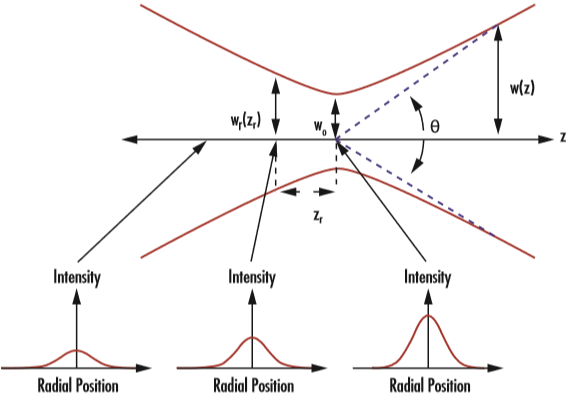
Figure 2: ガウシアンビームは、ビームウエスト (w₀)、レイリー領域 (z_R)、及び発散角 (θ) で定義される

ビームウエスト領域でのビーム径の変動は、次式によって定義されます：

(4)$$ w \! \left( z \right) = w_0 \sqrt{1 + \left( \frac{\lambda z}{\pi w_0 ^2} \right)^2} $$

ガウシアンビームのレイリー領域は、ビーム断面積が2倍になる地点のzの値として定義されます。これは、w (z)が√2w₀に増加した時に起こります。式4を用いて、レイリー領域 (z_R) は次のように表されます：

(5)$$ z_R = \frac{\pi w_0 ^2}{\lambda } $$

これにより、w (z) をz_Rの関数としても表されます：

(6)$$ w \! \left( z \right) = w_0 \sqrt{1 + \left( \frac{\lambda z}{\pi w_0 ^2} \right)^2} = w_0 \sqrt{1 + \left( \frac{z}{z_R} \right)^2} $$

レーザーの波面は、ビームウエストでは平面状で、ビームウエスト領域から離れるに従い、再度この形状に近づきます。これは、波面の曲率半径の大きさが無限大に近づき始めるためです。波面の曲率半径は、ビームウエストでの無限大をとり、そこから離れるに従い徐々に減少してレイリー領域で最小値をとり、そこから更に遠くに離れると無限大に戻っていきます (Figure 3)。これは、ビームウエストの両側について言えることです³ 。

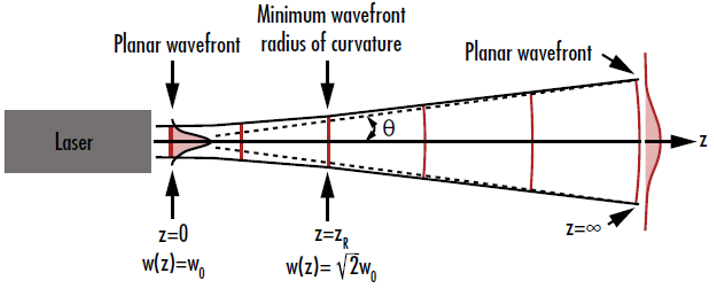
Figure 3: The curvature of the wavefront of a Gaussian beam is near-zero when it is both very close and very far away from the beam waist

Figure 3: ガウシアンビームの波面の曲率は、ビームウエスト近傍及びそこから極めて遠いところでほぼゼロになる

ガウシアンビームの操作

レーザー光学システムの多くは、「元々の」ビームを単純に用いるのではなく、レーザービームの操作を要求します。この操作は、レンズ、ミラー、プリズム等の光学部品を用いて行われるかもしれません。以下に、最も一般的なガウシアンビーム操作をいくつか紹介します。

ガウシアンビームに対する薄レンズの公式

理想的な薄レンズによる結像は、以下の公式を用いることができます²：

(7)$$ \frac{1}{s'} = \frac{1}{s} + \frac{1}{f} $$

式7において、s’はレンズから像までの距離、sはレンズから物体までの距離、fはレンズの焦点距離になります。物体と像がレンズに対して各々反対の位置にある時、sは負の値でs’は正の値をとります。この公式は、実物のレンズの厚さを無視しているため、現実世界の単なる近似になります (Figure 4)。 The thin lens equation can also be written in a dimensionless form by multiplying both sides of the equation by f:

(8)$$ \frac{f}{s'} = \frac{f}{s} + 1 \text{ or } \frac{1}{\left( \frac{s'}{f} \right)} = \frac{1}{\left( \frac{s}{f} \right)} + 1 $$

Figure 4: The thin lens equation allows the position of an image (s’) to be determined when the distance from the lens to the object (s) and the focal length of the lens (f) are known

Figure 4: 薄レンズの公式は、レンズから物体 (s) までの距離とレンズの焦点距離 (f) が分かれば、像 (s’) の位置を求めることができる

結像のアプリケーションでの適用に加え、この薄レンズの公式は、入力ビームのウエストを物体として、また出力ビームのウエストを像として扱うことで、ガウシアンビームの集光にも適用できます。ガウシアンビームは、収差のない理想的なレンズを通過した後でもガウシアン分布を維持します。1983年、Sidney Selfは、ガウス伝播を考慮に入れた薄レンズの新たな公式を作りました²：

(9)$$ \boxed{ \frac{1}{s'} = \frac{1}{ s + \frac{z_R ^2}{\left( s + f \right)}} + \frac{1}{f} } $$

レーザーから一点集光するまでの全距離は、sの絶対値をs’に加算することで計算されます。式9の両辺にfを乗算することで無次元の形式にも書き表すことができます：

(10)$$ \frac{f}{s'} = \frac{1}{\left( \frac{s}{f} \right) + \frac{\left( \frac{z_R}{f} \right)^2}{\left( \frac{s}{f} + 1 \right)} } + 1 $$

この公式は、z_R/fが0に近づくにつれて標準の薄レンズの公式に近づくため、長い焦点距離を持つレンズに対してその薄レンズの公式が使用できるようになります。式9と10は、レンズを通して像を結んだ後のビームウエストの位置を見つけるのに用いることができます (Figure 5)。

Figure 5: The ”object” when refocusing a Gaussian beam is the input waist and the “image” is the output waist

Figure 5: ガウシアンビームを再集光する際の「物体」が入力側ウエストに、「像」が出力側ウエストになる

A plot of the normalized image distance (s’/f) versus the normalized object distance (s/f) shows the possible output waist locations at a given normalized Rayleigh range (z_R/f) (Figure 6). This plot shows that Gaussian beams focused through a lens have a few key differences when compared to conventional thin lens imaging. Gaussian beam imaging has both minimum and maximum possible image distances, while conventional thin lens imaging does not. The maximum image distance of a refocused Gaussian beam occurs at an object distance of -(f + z_R), as opposed to –f. The point on the plot where s/f is equal to -1 and s’/f is equal to 1 indicates that the output waist will be at the back focal point of the lens if the input is at the front focal point of a positive lens.

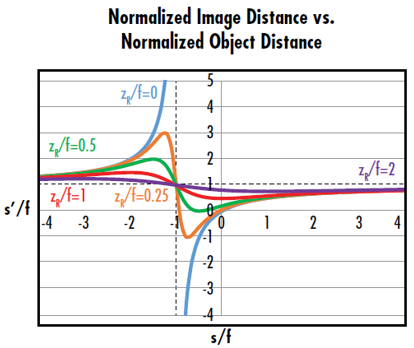
Figure 6: The curve where z<sub>R</sub>/f=0 corresponds to the conventional thin lens equation. The curves where z<sub>R</sub>/f>0 show that Gaussian imaging has minimum and maximum image distances defined by the Rayleigh range

Figure 6: The curve where z_R/f=0 corresponds to the conventional thin lens equation. The curves where z_R/f>0 show that Gaussian imaging has minimum and maximum image distances defined by the Rayleigh range

ビームがレンズを通過した後のビームウエストとレイリー領域を理解するには、次式で与えられるシステムの倍率 (α) を知っておく必要があります：

(11)$$ \alpha = \frac{w'_0}{w_0} = \frac{1}{\sqrt{\left(1 - \frac{s}{f} \right)^2 + \left( \frac{z_R}{f} \right)^2}} $$

ここで、w₀はレンズ通過前のビームウエスト、w₀’はレンズ通過後のビームウエストです。ガウシアンビームの薄レンズの公式は、レンズ通過後のビームのレイリー領域 (z_R’)を含めた形で次のように書き換えることができます：

(12)$$ \boxed{ \frac{1}{ s' + \frac{{z'}_R ^2}{\left( s' - f \right)} } = \frac{1}{s} + \frac{1}{f} } $$

上記公式は、レンズがビームウエストにある場合 (s=0) は、分解されます。倍率の自乗の逆数は、ビームウエストサイズと位置を関連付けるために用いることができます³：

(13)$$ \frac{1}{\alpha ^2} = \frac{ \left| s \right| - f}{s' -f} = \left( \frac{w_0}{w'_0} \right)^2 $$

ガウシアンビームの一点集光

レーザー材料加工や手術のようなアプリケーションの多くでは、強度を最大化しながら加熱エリアを最小化するため、レーザービームを可能な限り小さなスポットサイズに集光することが大変重要になります。この場合の目標は、w₀’を最小にすることです (Figure 7)。式13を変形したものが、出力側ビームウエストを最小にする方法を特定するのに用いることができます³：

(14)$$ \frac{\left( \left| s \right| -f \right)^2}{f^2 - \left( \frac{{w'}_0}{\theta} \right)^2 } = \left( \frac{w_{0}}{{w'}_0} \right)^2 $$

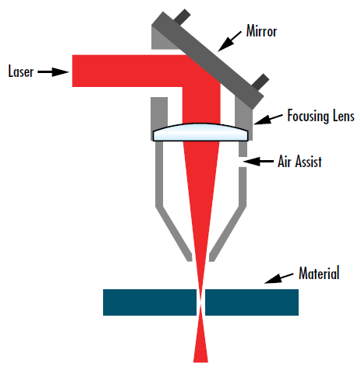
Figure 7: Focusing a laser beam down to the smallest possible size is crucial for a wide range of applications including this laser cutting setup

Figure 7: レーザービームを可能な限り小さなサイズに集光することは、レーザー切断を始めとする広範なアプリケーションに不可欠となる

式14の両辺に左辺の分母を乗算し、次に両辺を (w₀’)²で乗算すると、次式のようになります：

(15)$$ \left( \left| s\right| -f \right)^2 = f^2 \left( \frac{w_0}{w'_0} \right)^2 - \left( \frac{w_0}{\theta} \right)^2 = f^2 \left( \frac{w_0}{w'_0} \right)^2 - z_R ^2 $$

(16)$$ \left( w'_0 \right) ^2 \left[ \left( \left| s \right| - f \right)^2 + z_R ^2 \right] = f^2 w_0 ^2 $$

上の式をw₀'に関して解くと次式のようになります：

(17)$$ \boxed{ w'_0 = w_0 \frac{f}{\sqrt{\left( \left| s \right| - f \right) ^2 + z_R ^2}} = \alpha w_0 } $$

(18)$$ \boxed{ \alpha = \frac{f}{\sqrt{\left( \left| s \right| -f \right)^2 + z_R ^2}} } $$

集光したビームウエストは、レンズの焦点距離と |s|-f を小さくすることで最小にすることができます。式17の w₀ に隣接する項は、入力ビームの値をレンズ通過後の出力側ビームの値と比較するため、倍率定数αを用いた別の形式として表されます (Figure 8)³。

(19)$$ \theta ' = \frac{\lambda}{\pi w'_0} = \frac{\lambda}{\pi \alpha w_0} = \frac{\theta}{\alpha} $$

(20)$$ z'_R = \frac{w'_0}{\theta '} = \frac{\alpha w_0}{\left( \frac{\theta}{\alpha} \right)} = \alpha ^2 z_R $$

(21)$$ \boxed{ s' = f + \alpha ^2 \left( \left| s \right| - f \right)} $$

Figure 8: For a magnification of 2, the output beam waist will be twice the input beam waist and the output divergence will be half of the input beam divergence

Figure 8: 倍率αが2の時、出力側ビームウエストは入力側ビームウエストの2倍になり、出力側発散角は入力側発散角の半分の大きさになる

出力側ビームウエストのサイズと位置の計算をよりシンプルにする2つの特異なケースがあります。それは、sがz_Rよりも遥かに小さい場合と、sがz_Rよりも遥かに大きい場合です³。レンズがレーザーのレイリー領域内にある時、s << z_Rかつ (|s|-f)² <z_R² となります。これにより、式18は次のシンプルなものになります：

(22)$$ \alpha = \frac{f}{z_R} = \frac{f \theta}{w_0} $$

これにより、出力側ビームのウエストや発散角、レイリー領域やウエスト位置の計算もシンプルになります：

(23)$$ \theta ' = \frac{\theta}{\alpha} = \frac{ \theta w_0}{f \theta} = \frac{w_0}{f} $$

(24)$$ z_R ' = \alpha ^2 z_R = \frac{f^2}{z_R ^2} z_R = \frac{f^2}{z_R} $$

(25)$$ \boxed{ w'_0 = \alpha w_0 = f \theta } $$

(26)$$ \boxed{ s' = f + \alpha^2 \left( \left| s \right| - f \right) = f + \frac{ \left| s \right| f^2}{z_R ^2} \approx f } $$

s << z_Rの時、レンズから集光スポットまでの距離はレンズの焦点距離に等しくなります。

他の特異な状況は、レンズがレイリー領域の遥か外に配置され、s >> z_Rになる時、式18は次のシンプルなものになります：

(27)$$ \alpha = \frac{f}{\left| s \right|} $$

(28)$$ w'_0 = \frac{f w}{ \left| s \right|} $$

s << z_R である時と同様に、出力側のビームウエストや発散角、レイリー領域やビームウエスト位置の計算もシンプルなものになります：

(29)$$ \theta ' = \frac{\theta}{\alpha} = \frac{\left| s \right| \theta }{f} $$

(30)$$ z'_R = \alpha^2 z_R = \frac{f^2 z_R}{s^2} $$

(31)$$ \boxed{ w'_0 = \alpha w_0 = \frac{fw_0}{\left| s \right|} } $$

(32)$$ \boxed{ s' = f + \alpha ^2 \left( \left| s \right| - f \right) = f + \frac{\left( \left| s \right| - f \right) f^2}{s^2} = f + \frac{f^2}{ \left| s \right|} \approx f } $$

s >> z_R の時、レンズから集光スポットまでの距離はレンズの焦点距離に等しくなります。

ビームウエストとそこから大きく離れた位置ではビーム波面がほぼ平面になることから、この両方の結果は直感的に理解できるものです。これらの位置では、ビームはほぼ完全にコリメートされています (Figure 9)。標準の薄レンズの公式では、コリメートされた入力ビームの像距離はレンズの焦点距離に等しくなります。

Figure 9: The focused spot of a Gaussian beam after it passes through a lens will be located at the focal point of the lens if the input beam waist is either very close or very far away from the lens. This is because the input beam is approximately collimated at those points

Figure 9: レンズ通過後のガウシアンビームの集光点は、入力側ビームウエストがレンズに極めて近いか、あるいはレンズから非常に離れている場合に、レンズの焦点に位置する。これは、入力側ビームがこうした地点ではほぼコリメートになるためである

ガウシアン焦点シフト

直感的にわかりづらいことですが、レンズからある一定距離 (L) にある標的上に像を結ぶ集光ビームの強度は、ウエストが標的上にある場合でも最大にはなりません。実際は、ウエストが標的手前のある場所に位置する時に、標的上での強度が最大になります (Figure 10)。この現象は、ガウシアン焦点シフトとして知られています。

Figure 10: The minimum beam radius at a target occurs when the waist of the focused beam occurs at a specific location before the target, not when focused waist is located at the target

Figure 10: ビーム半径が標的上で最小になるのは、一点集光するビームのウエストが標的上ではなく、標的手前の特定の場所にある時に生じる

本テキストでは式の導出を延々と述べませんが、標的上でのビーム半径は次式のように記述することができます⁴:

(33)$$ w_L = \frac{w_0}{z_R} \left[ f^2 - 2 \left( \left| s \right| - f \right) \left( L - f \right) + \left( \frac{L-f}{\alpha} \right)^2 \right] $$

式34を、集光レンズの焦点距離 (f) で微分し、d/df [w_L (f)]=0 としてfを解くと、ビーム半径が最小となるレンズの焦点距離、即ち標的上で最大強度が得られる焦点距離が導き出せます。

(34)$$ \frac{ \text{d} }{ \text{d}f } \left[ w_L \! \left( f \right) \right] = \frac{w_0}{z_R} \left[ 2f + \left( \left| s \right| -f \right) +2 \left( L - f \right) - \frac{2 \left( L - f \right)}{\alpha ^2} \right] $$

(35)$$ \frac{ \text{d} }{ \text{d}f } \left[ w_L \! \left( f \right) \right] = 0 \text{ when } f = \left( \frac{1}{\left| s \right| + \frac{z_R ^2}{\left| s \right|}} + \frac{1}{L} \right) ^{-1} $$

f = L の時、|s| がゼロまたは無限大に近づくと、d/df [w_L (f)]=0 になります。この両方のケースにおいても入力側ビームはほぼコリメートになるため、レンズの焦点上で最小ビーム半径が得られることになります。

Collimating a Gaussian Beam

Achieving a truly collimated beam where the divergence is 0 is not possible, but achieving an approximately collimated beam by either minimizing the divergence or maximizing the distance between the point of observation and the nearest beam waist is possible. Since the output divergence is inversely proportional to the magnification constant α, the output divergence reaches a minimum value when |s| = f (Figure 11).

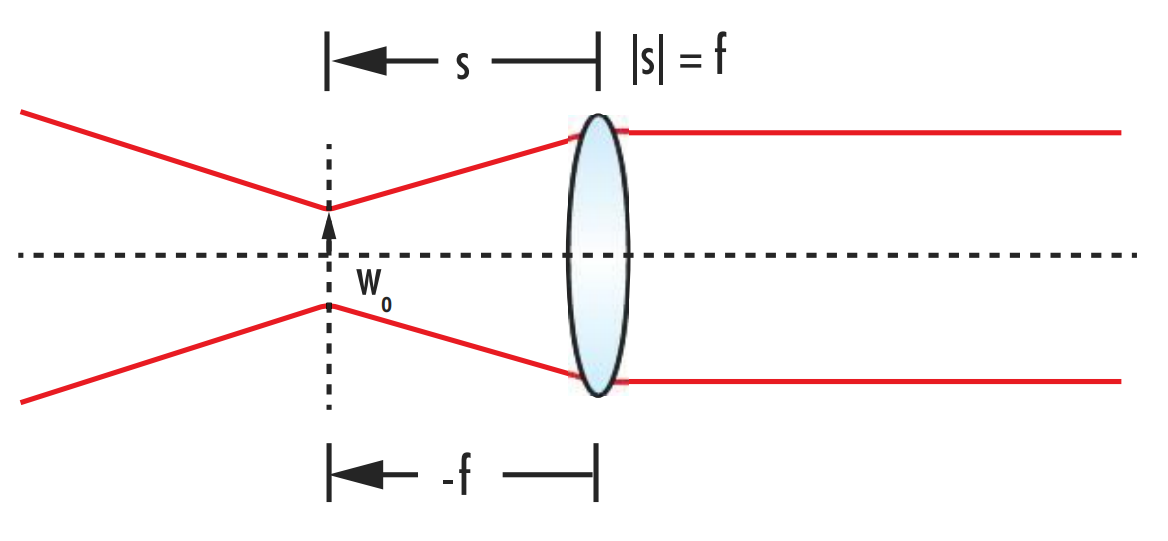
Figure 11: To collimate a Gaussian beam, the distance from the beam waist to the collimating lens should be equal to the lens’ focal length

参考文献

Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
Self, Sidney A. “Focusing of Spherical Gaussian Beams.” Applied Optics, vol. 22, no. 5, January 1983.
O'Shea, Donald C. Elements of Modern Optical Design. Wiley, 1985.
Self, Sidney A. “Focusing of Spherical Gaussian Beams.” Applied Optics, vol. 22, no. 5, Jan. 1983.
Katz, Joseph, and Yajun Li. “Optimum Focusing of Gaussian Laser Beams: Beam Waist Shift in Spot Size Minimization.” Optical Engineering, vol. 33, no. 4, Apr. 1994, pp. 1152–1155., doi:10.1117/12.158232.

前のセクション次のセクション Next Section

その他の資料