ビーム品質とストレール比

本ページはレーザーオプティクスリソースガイドのセクション4.2, 4.3, 4.4, 4.5, 4.6です

レーザーの現実世界の性能や品質を正確に予測するために、ビームの形状を説明するレーザーの共振器モードやビームの品質を説明するM²値を理解する必要があります。レーザーの性能が分かれば、それと一緒に用いる光学系の真の性能を特徴づけることで最終的なシステム性能の理解が可能になります。光学系の現実の性能とその理想的性能、即ち回折限界性能との比較は、ストレール比を用いることで行われます。

M² 因子

レーザーのビーム品質は、ビームの実際の形状と理想的なガウシアンビームの形状を比較したM²因子によって表されます。ISO規格11146では、M²因子を次式のように定義しています¹：

(1)$$ M^2 = \frac{\pi w_0 \theta}{\lambda} $$

式1において、w₀はビームウエスト、θはレーザーの発散角、λは発振波長です (Figure 1)。ガウシアンビームの伝播で定義されている通り、ガウシアンビームの発散角は次式によって決まります：

(2)$$ \theta = \frac{\lambda}{\pi w_0} $$

この式で決定される発散角を式1に代入すると、ガウシアンビームのM²因子の公式を簡単に表せます：

(3)$$ M^2 = \frac{\pi w_0}{\lambda} \times \frac{\lambda}{\pi w_0} = 1 $$

Figure 1: レーザービームの発散角とビームウエスト

この結果、1のM²因子は、回折限界のガウシアンビームに該当します。M²因子が (1より) 大きくなると、理想的ガウシアンビームからずれることを意味しています。1未満の値にはなり得ません。エルミート・ガウシアンモードのM²因子は、x方向が (2n + 1)、y方向が (2m + 1) で与えられます²。例えば、TEM₁₃はx方向で3、y方向で7のM²因子を持ちます。代表的なHe-Neレーザーは、1から1.1のM²因子があります。More information on Hermite-Gaussian Modes can be found in our Laser Resonator Modes application note.

レーザービームの光学的パワー以外に、M²因子はビームの輝度も決定します。M²因子は、レーザーの波長をガウシアンビームの伝播の公式全てに見られるM²因子と波長の積の値で置き換えることで、ビームが伝搬する間のビーム半径の近似にも用いることができます³。

M²因子は、ある発散に対してレーザービームがどの程度集光することができるかを表す重要なパラメータです。M²因子が小さくなると、より締まった集光になり、ビームがもつパワーをより効率良く使用し、レーザーの潜在的実効パワーをより大きくすることができます。

M²因子の測定は、レーザー軸上の一平面でビーム形状を計測するのと違い、シンプルではありません。ISO 11146では、ニアフィールドとファーフィールドの両方において、光軸に沿った別々の位置で5回、ビーム半径測定を行うことを規定しています⁴。ビームにTEM₀₀モードが全く含まれていなくても、そのビームをある特定面で理想的なガウシアンであるように見せることは可能です (Figure 2)。この特定面での断面が完全なガウシアン分布のように見えたとしても、そのビームはガウシアンビームとは全く異なる伝播を行い、より大きな発散角を持つようになります⁵。異なる平面での複数回の半径測定により、このビームと真のガウシアンビーム間の違いはすぐに明らかになることでしょう。測定されたビーム半径 (w(z)) は、次式のようにビームウエスト (w₀)、波長 (λ)、及びM²因子に関連付けることができます⁶：

(4)$$ w \! \left( z \right) ^2 = w^2 _0 \left[ 1 + \left(z - z_0 \right)^2 \left( \frac{M^2 \lambda}{\pi w_0 ^2} \right)^2 \right] $$

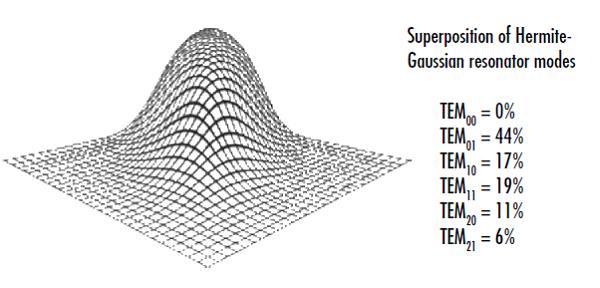
Figure 2: This beam cross-section appears Gaussian at a specific plane even though it doesn’t contain any of the TEM00 mode, illustrating the importance of making several intensity measurements along the laser axis to determine a laser’s M<sup>2</sup> factor

Figure 2: このビーム断面は、TEM₀₀モードが全く含まれていないにもかかわらず、ある面では理想的なガウシアンのように見えている。このことは、レーザーのM²因子を決定する際に、レーザー軸に沿って強度測定を複数回行うことの重要性を表している

他のビーム品質パラメータと比較し、M²因子を用いてビームを特徴づけるデメリットの一つに、中心から一番遠く離れた低パワー密度のビーム部分、即ち“ウイング”上をより強調してしまう点があります。

ビームパラメータ積

ビームパラメータ積 (BPP) は、レーザービームの品質を評価するのに用いられる別の基準であり、ビームウエストでのビーム半径とビーム発散半角の積で定義されます。一般的に mm・mrad の単位で表され、次式のようにM²因子に関係しています：

(5)$$ \text{BPP} = \frac{M^2 \lambda}{\pi} $$

BPPはM²因子に正比例するので、ビームパラメータ積が大きいほどビーム品質は悪くなります。BPPの最小値はλ/πで、これは理想的なガウシアンビームでのみ得られる値になります。

BPPは、大きなM2因子をもつファイバーレーザーか半導体レーザーの特徴づけ、あるいはファイバーカップリングしたダイオードレーザーシステムなど、ファイバー内にカップリングできる光量を決定するのに共通して用いられます。

Power in the Bucket (バケット内パワー)

Power in the bucket (PIB) は、ビーム品質を定義するもう一つの基準で、ハイパワーレーザーシステムや材料加工のアプリケーションに良く用いられます。PIBは、特定「バケット (bucket)」に対して収まっているレーザーパワーを表し、ここでいうバケットとは、加工される面における特定スポット半径を通常指しています。これは一見単純なコンセプトに見えますが、ファーフィールドでのバケットの形状が適切に定義され、ニアフィールドでのビーム形状の仕様に依存した理想的シナリオと比較できるようにしなければなりません。
PIBに対する正確な業界標準規格はありませんが、多くは垂直または水平方向のビーム品質のどちらかで報告されています⁷：

(6)$$ \text{Vertical Beam Quality} = \sqrt{\frac{\text{Ideal Power in Bucket}}{\text{Actual Power in Same Bucket}}} $$

(7)$$ \text{Horizontal Beam Quality} = \frac{\text{Actual Beam Radius at a Given Power}}{\text{Ideal Beam Radius at the Same Power}} $$

M²因子やBPPと同様に、PIB値が小さいことはビームの品質が高いことを意味します。PIBは、所定の「バケット (bucket)」内でのパワーの分数をλ/Dの関数としてプロットすることで見える化できます。ここで、Dはニアフィールドビームの直径です (Figure 3)。垂直ビーム品質は、所定のλ/Dにおけるバケット内での理想的ガウシアンビームのパワーと現実のビームのそれの比率の平方根となり、それがプロットの垂直方向の寸法に対応します。同様に、水平ビーム品質は、バケット内の理想的ガウシアンビームのλ/D値と現実のビームのそれの比率となり、それがプロットの水平方向の寸法に対応します。

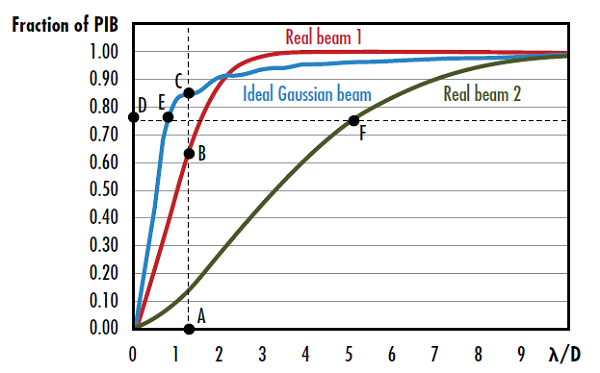
Figure 3: The vertical beam quality of real beam 1 is given by square ratio of the ratio of segment AC to segment AB and the horizontal beam quality of real beam 2 is given by the ratio of segment DF to segment DE7

Figure 3: Real beam 1の垂直ビーム品質はACとABの比率の平方根で与えられ、Real beam 2の水平ビーム品質は、DFとDEの比で与えられる⁷

真円ビーム vs. 楕円ビーム

レーザービームの形状を考える時、レーザーが真円ビームと楕円ビームのどちらを出射するかを理解することが重要です。半導体レーザーダイオードは、活性領域が正方形ではなく矩形であることから、x方向とｙ方向で発散角の異なる楕円形状ビームを出射します (Figure 4)。開口が小さくなると回折が大きくなるため、活性領域の短い方向では発散角がより大きくなり、結果として非点隔差ビームを作り出します。大きな発散角を持つ軸がファスト軸、それに対して小さな発散角を持つ軸がスロー軸と定義されます。シリンダーレンズは、楕円ビームを真円化するのによく用いられます (Figure 5)。シリンダーレンズに関する更なる情報は、レーザービーム整形の概要をご覧ください。

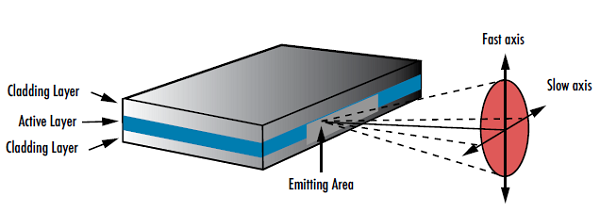
Figure 4: The geometry of laser diodes causes them to produce elliptical beams with two different divergence angles

Figure 4: レーザーダイオードの形状は、2つの異なる発散角を持つ楕円形ビームを作り出してしまう

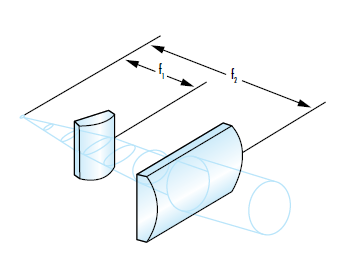
Figure 5: Cylinder lenses are often used to circularize an elliptical beam by acting on the fast and slow axes separately

Figure 5: シリンダーレンズは、ファスト軸とスロー軸に別々に作用し、楕円ビームの真円化によく用いられる

ストレール比

M²因子がレーザーの現実の性能を理想的ビームと比較しているのと同様に、光学系または光学部品のストレール比は、その現実の性能と理想的な性能の比較になります。球面や非球面レンズを始めとする集光用オプティクスのストレール比は、実際のオプティクスが点光源から一点集光した時の最大放射強度と、理論的な回折限界を持つオプティクスを用いて一点集光した時の理想的強度の比になります (Figure 6)^7&。ストレール比が1だとそのオプティクスは完璧で、収差フリーになります。業界で一般化している慣例として、ストレール比が0.8を超えていれば、そのレンズは「回折限界」と見なされます。

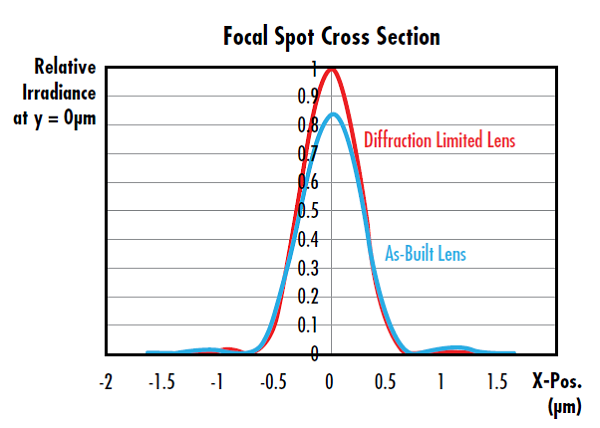
$Figure 6: This lens has a Strehl Ratio of 0.826, which is considered diffraction limited because it is greater than 0.8.$

Figure 6: このレンズのストレール比は0.826で、0.8を超えていることから、回折限界であると考えられる

オプティクスのストレール比とRMS透過波面誤差のおおよその関係は、公式 8で表されます。ここで、Sはオプティクスのストレール比、σはオプティクスのRMS波面誤差です⁸。この近似式は、波面誤差が0.2波長未満の時に成立します。

(8)$$ S = \exp{\left[ - \left( 2 \pi \sigma \right)^2 \right]} $$

オプティクスの面の不規則性がそのストレール比にどのような影響を及ぼすかに関する情報は、非球面レンズのイレギュラリティとストレール比をご覧ください。

参考文献

International Organization for Standardization. (2005). Lasers and laser-related equipment – Test methods for laser beam widths, divergence angles and beam propagation ratios (ISO 11146).
A. E. Siegman, “New developments in laser resonators”, Proc. SPIE 1224, 2 (1990)
Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
International Organization for Standardization. (2005). Lasers and laser-related equipment — Test methods for laser beam widths, divergence angles and beam propagation ratios — Part 1: Stigmatic and simple astigmatic beams (ISO 11146-1:2005).
A. Siegman, “’Non-Gaussian’ Beam”, OSA Annual Meeting, Long Beach, CA (1997)
Hofer, Lucas. “M² Measurement.” DataRay Inc., 12 Apr. 2016, www.dataray.com/blog-m2-measurement.html.
Strehl, Karl W. A. “Theory of the telescope due to the diffraction of light,” Leipzig, 1894.
Mahajan, Virendra N. "Strehl ratio for primary aberrations in terms of their aberration variance." JOSA 73.6 (1983): 860-861.